Na tytułowe pytania zazwyczaj odpowiadają sobie studenci matematyki, a nie brydżyści. Bo i odpowiedź na nie ma większego zastosowania praktycznego.
Wszystkie źródła za każdym razem podają liczbę:

Objaśniam: pierwszy dwumian newtonowski to liczba możliwości wybrania 13 kart z 52 dla pierwszej ręki (dla przykładu N), drugi dla drugiej (w przykładzie E), trzeci dla trzeciej (w przykładzie S), czwarty… równa się jeden, bo ostatnia ręka (W) zostanie przydzielona „z automatu”.
Ale zdecydowana większość studentów i profesorów matematyki w brydża niestety nie gra i wszędzie powtarzana odpowiedź jest tak naprawdę niepoprawna!
Zgodnie z formalnymi przepisami, każdy układ 52 kart może wystąpić w 16 kombinacjach – każdy z 4 graczy może być rozdającym („Dealerem”), a także mogą wystąpić 4 rożne rodzaje założeń: obie przed partią, NS po partii, EW po partii i obie po partii. A to oznacza, że powyższą liczbę należy pomnożyć jeszcze przez 16! Tak więc, liczba możliwych rozdań w brydżu to tak naprawdę:
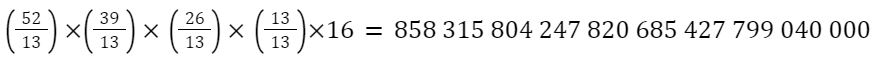
czyli 858 kwadryliardów z dodatkami.

Tak to jest gdy brydżysta zajmie się matematyką.
Brzmi to może jak niepotrzebna komplikacja, ale warto z tego zapamiętać, że jeśli na przykład na turnieju źle włożymy karty do pudełka (obrócone o 90 lub 180 stopni), to zmieni się „Dealer”, a czasem również założenia i w myśl przepisów gry w brydża będzie to już zupełnie inne rozdanie.
Z innych ciekawostek – liczba możliwych rąk, które może otrzymać jeden gracz to:
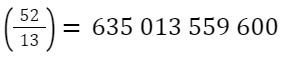
Tylko miliardy, spadliśmy na ziemię.

Czasami o bardzo doświadczonych brydżystach mówi się, że „grają już drugie koło”, a oni lubią żartować, że dane rozdanie „już kiedyś widzieli”. Czysto teoretycznie takie zdarzenie jest możliwe, chociaż większość śmiertelników nigdy nie dostanie nawet dwa razy tej samej ręki, a co dopiero roztasować wszystkie 52 karty tak samo…

Jeśli komuś mało, to liczba możliwych licytacji w brydżu chyba już przebija sufit:
128 745 650 347 030 683 120 231 926 111 609 371 363 122 697 557
Powyższe 128 septyliardów to, bagatelka, 150 biliardów razy więcej niż możliwych rozdań.
Tak więc to w licytacji mamy największe pole do popisu. Tylko dlaczego ciągle licytujemy: 1BA – 3BA?
Maciej Kędzierski


Bardzo fajna inspiracja intelektualna
Ciekawa jest interpretacja graficzna tej ilości rozdań. Gdyby jedno rozdanie miało grubość 1 mm, i gdyby je wszystkie położyć na sobie, to na jaką odległość by sięgnęły?
Typowe odpowiedzi to: do księżyca, może do słońca.
Byłoby trochę dalej. Na odległość 5,5 miliardów lat świetlnych!!! Mogłem się trochę pomylić, bo to z pamięci. Ale nie dużo. Łatwo to sprawdzić. Nawet kalkulatorem.